This was originally a story written to my imaginary/sworn(?) elder sister and her daughter in Singapore.
It began with "Hello, ..., It's long time since..."
NOTE: In this article, we discuss a possible side channel attack (of gniibe). Although we discuss the vulnerability by an atack, we don't show the concrete implementation of the attack itself (but only pseudo code which sketches the attack). Please go to Appendix: Don't Do That! for some knowledge for side channel attacks.
Monty Hall problem
Ever heard of "Monty Hall problem" [1] or Marilyn vos Savant?
The game is simple:
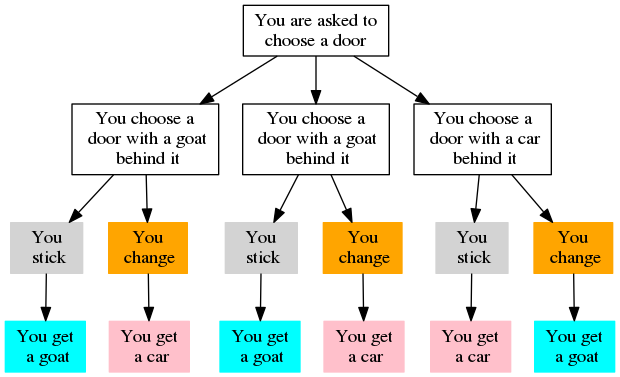
Suppose you’re on a game show, and you’re given the choice of three doors. Behind one door is a car, behind the others, goats. You pick a door, say #1, and the host, who knows what’s behind the doors, opens another door, say #3, which has a goat. He says to you, "Do you want to pick door #2?" Is it to your advantage to switch your choice of doors? [2]
| [1] | https://en.wikipedia.org/wiki/Monty_Hall_problem |
| [2] | http://marilynvossavant.com/game-show-problem/ |
I considered that it's pretty good problem to program a computer simulation, since statistics is better than debate. So, I code.
I don't call the doors by numbers, but call 'R', 'B', and 'G' from now on (you can consider it's Red, Blue, and Green). That's because number starts from 0 for me, but, it starts from 1 in the original game description, which is error-prone.
Five Strategies
Here, I considered five players and each player has different strategies.
Nobita
Nobita randomly chooses a door and never switches his decision.
Chuji
Chuji randomly chooses a door and randomly switches his decision.
Marilyn
Marilyn randomly chooses a door and always switches her decision.
Tetsuya
Tetsuya always chooses the door B at first and always switches his decision after host opens another door.
Budai
Budai randomly chooses a door among R and B and switches his decision if host doesn't open B.
Guess who will be a winner?
Certainly, it will be Marilyn.
But, Tetsuya will tie, and I like his strategy best, because it's like real gambler's one.
Although Budai is not a winner, I like his humble expectation best.
Computer simulation
Here is a result by my computer simulation. The trials are 1 million games. The argument (string 'number...') specifies random seed to be reproducible trials. You can omit this string, then, the seed will be system time.
$ python monty_hall_problem.py 'number is better than debate'
Random seed: "number is better than debate"
Player Success
------------------------
Nobita 333708
Chuji 500405
Marilyn 666424
Tetsuya 666417
Budai 583001
Well, any person can mount this result to put her own interpretation. However, I don't give you any explanation, but only numbers. It's you who interpret this.
Bias makes Tetsuya win
When you are the side of game host, you must consider using good Random-Bit-Generator (RBG) to guarantee fairness.
And you also need to care about handling of RBG.
At the first stage, host needs to choose a door among three to put a car behind it. Because there are three candidates, two bits are required at minimum.
Then, Easy implementation of 0 to 2 RNG would do:
- Get two bits from RBG.
- Calculate a modulo three
But, this is wrong. Totally wrong.
The generated random numbers will have severe bias and 0 will be generated with 50% probability (instead of 1/3).
With this biased random choice of doors, Tetsuya will win. Let's see by another computer simulation (option '-b' selects biased random door):
$ python monty_hall_problem.py -b 'number is better than debate'
Random seed: "number is better than debate"
Player Success
------------------------
Nobita 332155
Chuji 499506
Marilyn 666144
Tetsuya 749574
Budai 625009
Tetsuya wins 75%. Budai's success is also increased.
Perhaps, Tetsuya and Budai know there are bias in many implementations, in practice.
Proper implementation should do something like:
- Get a two bits from RBG.
- If it's 11, go to (1), or else return the bits
You see, we need more entropy.
Side channel attack by gniibe
In June 2015, which is the birth month of his imaginary _elder_ sister in Singapore, gniibe, a wanabee hacker in Japan, discovered an effective side channel attack against an implementation of this game.
According to gniibe, he can guess 100% time if an implementation of the game is not good enough.
In the section above (Bias makes Tetsuya win), we considered an issue for handling of RBG output. It was related to the first choice of a door by host.
In this case, it is related to the second choice of a door (to open) by host.
Host should be fair, so, an implementation could/should use RBG to choose a door for this second stage. Note that host always opens a door with a goat. Thus, RBG for choice is only required when the first choice by a player is correct. Or else, host's choice will be determined (other door: not the player's choice, not the door with a car).
gniibe's attack mounts this fact. Host's access to RBG to open a door means player's first choice was correct.
Let's see his strategy in Python.
class gniibe(Tetsuya):
def __init__(self, rbg_of_host):
Tetsuya.__init__(self)
self.rbg = rbg_of_host
def decision_first(self):
self.observed_counter = self.rbg.examine()
return Tetsuya.decision_first(self)
def decision_second(self, opened_door):
increment = self.observed_counter - self.rbg.examine()
return not (increment == 0)
The class 'gniibe' inherits Tetsuya's strategy. The important thing in his strategy is that he has access to RBG (side channel) information, although he cannot access to the output of RBG itself.
His first decision is as same as Tetsuya's. But, he records the RBG information here and uses this for his second decision.
His second decision is based on observed change of RBG counter. When RBG is not accessed by host for the choice of host's opening a door, gniibe's answer will be False. When RBG is accessed by host, gniibe's answer will be True.
Here we go the simulations. Option -g enables to show gniibe's attack.
$ python monty_hall_problem.py -g 'number is better than debate'
Random seed: "number is better than debate"
Player Success
------------------------
Nobita 333708
Chuji 500405
Marilyn 666424
Tetsuya 666417
Budai 583001
gniibe 0
$ python monty_hall_problem.py -g -b 'number is better than debate'
Random seed: "number is better than debate"
Player Success
------------------------
Nobita 332155
Chuji 499506
Marilyn 666144
Tetsuya 749574
Budai 625009
gniibe 0
Yeah, he always (100%) gets a goat, which is his favorite (you'd say it's cognitive distortion of Zen Buddhist)! Bias in the first stage doesn't matter.
To mitigate this attack, host should always access RBG even if it will be non-use.
You see, we need more entropy. Again.
Appendix: Another case, fixed but biased
Let's see if host knows the attack and he fixed the implementation. That is, host always accesses RBG even if the choice is determined.
Suppose host forgot to fix the bias issue of RBG handling. Here is the simulation result.
$ python monty_hall_problem.py -g -b -f 'number is better than debate'
Random seed: "number is better than debate"
Player Success
------------------------
Nobita 333456
Chuji 500079
Marilyn 666821
Tetsuya 749578
Budai 624845
gniibe 749679
See, gniibe will get a car with 75% probability in this configuration.
Well, it's also good for him, actually. We know that gniibe could enjoy either cases of best and worst.
Appendix: Books and papers
We can find the Monty Hall problem and the story of Marily vos Savant in [3] (Japanese Translation is [4]). This book is very interesting to read. I recommend.
The problem can be found in [5] by different expression, too. From same publisher, I rather recommend [6] or [7] but the latter is hard to get today.
For Chuji, [8] is the definite research, but it was only published by 500 copies. You can find this book in the Gunma prefectural library.
For Budai/Tetsuya and his philosophy, please read [9]. In fact, Tetsuya is an alias of Budai.
When you enjoy Dr. Seki's book, you might want to read the papers by S. O. Rice [10] [11], too.
| [3] | Leonard Mlodinow, The Drunkard's Walk: How Randomness Rules Our Lives, Pantheon Books, 2008 |
| [4] | 田中三彦訳, たまたま: 日常に潜む「偶然」を科学する, ダイヤモンド社, 2009 |
| [5] | 竹内 啓, 偶然とは何か――その積極的意味, 岩波新書, 2010 |
| [6] | 木田 元, 偶然性と運命, 岩波新書, 2001 |
| [7] | 関 英男, 雑音, 岩波全書, 1954 |
| [8] | 橋田 友治, 国定忠次の再研究, 伊勢崎郷土文化協会, 1986. |
| [9] | 色川 武大, 色川武大阿佐田哲也全集(2), 福武書店, 1992. |
| [10] | Stephen O. Rice, Mathematical Analysis of Random Noise, Bell Systems Tech. J., Volume 23, p. 282-332, 1944 |
| [11] | Stephen O. Rice, Mathematical Analysis of Random Noise - Conclusion, Bell Systems Tech. J., Volume 24, p. 46-156, 1945 |
| [12] | 鈴木 大拙, 日本的霊性 (完全版), 角川ソフィア文庫, 2010. |
Appendix: Code
The code in Python and it's titled: Monty Hall problem simulation
Appendix: Don't Do That!
Although I explained how an attack impacts the game, I don't explain how we can implement.
Please refer following papers for such technology. Those attacks were effective and I had to fix the implementation of GnuPG and libgcrypt.
| [13] | Yuval Yarom and Katrina Falkn
|
| [14] | Fangfei Liu, Yuval Yarom, Qian Ge, Gernot Heiser and Ruby B. Lee
|
| [15] | Daniel Genkin, Adi Shamir and Eran Tromer
|
| [16] | Daniel Genkin, Itamar Pipman and Eran Tromer
|
| [17] | Daniel Genkin, Lev Pachmanov, Itamar Pipman and Eran Tromer
|
Appendix: Explanations
Sister and readers suggested to have explanations, so, here we go.
Easy implementation of 0 to 2 RNG
The implementation of this kind of RNG is typical. It's common mistake. That's because people consider that two bits are enough to represent three, and computation is done easily by modulo operation.
Here is a table to see the bias.
| From RBG | Modulo 3 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 0 |
Given the original RBG generate equally, it results that 0 will be generated 50% (while 1 and 2 will be generated 25% each).
 GNU wannabee and Happy Hacking
GNU wannabee and Happy Hacking